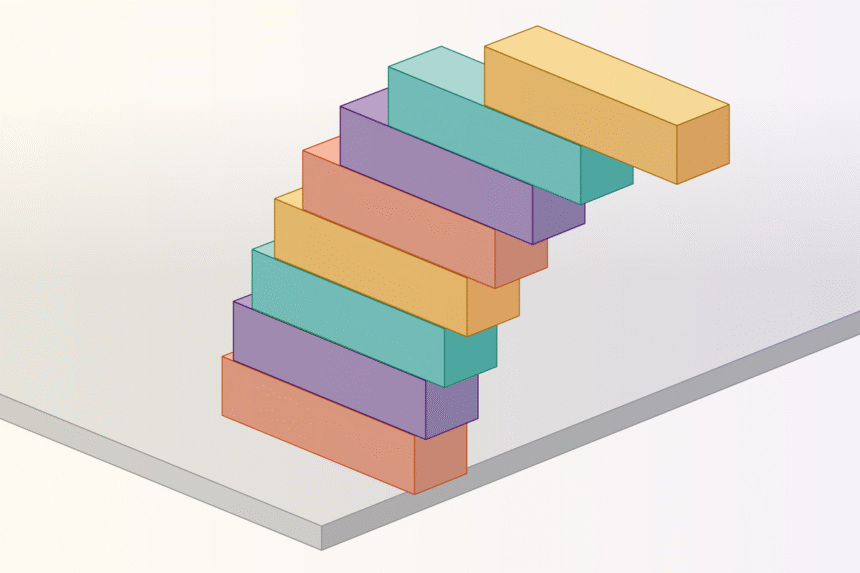
The overhang distance of the top block decreases by half with each block added to the tower. For example, with three blocks, the top block can only extend one-eighth of its length beyond the block below it. With four blocks, it’s just one-sixteenth, and so on. This pattern holds true for any number of blocks you stack, no matter how high the tower reaches.
Mathematically, this phenomenon can be explained using the concept of a harmonic series. This series is an infinite sum of fractions where each term is the reciprocal of a natural number. In the case of our block-stacking problem, each block extends only half of the distance of the block below it. This creates a harmonic series where each term is half of the previous one. As we add more blocks to the tower, the total overhang distance approaches a limit that is not finite.
In an idealized world with perfectly uniform blocks and no external forces, this stack of blocks can theoretically extend infinitely. Imagine a bridge made of blocks that stretches across the Grand Canyon, with each block only partially supported by the one below it. It’s a mind-bending concept that challenges our intuition about balance and stability.
While this block-stacking problem may seem like a whimsical exercise, it actually illustrates some fundamental principles of physics and mathematics. The idea of a center of mass and the concept of a harmonic series are powerful tools that scientists and engineers use to understand and predict the behavior of complex systems.
So next time you’re playing with children’s blocks, take a moment to appreciate the intricate physics behind a seemingly simple stacking game. Who knows, you might just uncover some preposterous solutions that will leave you in awe of the wonders of science and mathematics. The concept of stacking blocks might seem simple at first glance, but when you dive deeper into the mathematics behind it, things get a lot more interesting. The idea that each block in a tower extends a fraction beyond the one below it creates a fascinating pattern that has intrigued mathematicians and physics enthusiasts alike.
Let’s take a closer look at how this phenomenon works. Imagine a tower of blocks where each block extends a specific fraction beyond the block below it. For example, the top block extends 1/2 of a unit, the second block extends 1/4, the third extends 1/6, and so on. This pattern continues indefinitely, with each subsequent block extending by a smaller fraction than the one before it.
To illustrate this concept, let’s consider a tower with five blocks. If we add a sixth block below it and try to slide the entire structure out as far as possible, we can analyze the behavior of the tower by looking at the mass distribution. By treating the tower as two blocks – one with a mass of 5 on top of a block with a mass of 1 – we can understand how the blocks interact.
When we try to maximize the overhang of the tower, we need to balance the centers of mass of the two blocks. The heavier block needs to be pushed farther out than the lighter block to maintain equilibrium. This principle, known as the law of the lever, explains how the overhang distance changes based on the relative masses of the blocks.
In this scenario, the top block extends 1/12 of a unit beyond the edge, while the bottom block extends 5/12. By calculating these distances at each level of the tower, we can determine the correct overhang for the entire structure.
As we add more blocks to the tower, the total overhang distance becomes the sum of all the individual overhangs. For a tower with 10 blocks, the overhang would be approximately 1.464 block lengths beyond the edge. This pattern of adding up shrinking terms resembles the harmonic series in mathematics, where the sum of reciprocal fractions converges to a finite value.
In the case of the block-stacking problem, each overhang corresponds to half of a term in the harmonic series. Since the harmonic series grows infinitely but very slowly, the potential overhang of the tower has no limit. This means that with enough blocks, you could theoretically extend the top block indefinitely beyond any surface.
While this theoretical concept is intriguing, practical applications face challenges due to real-world physics. Balancing a tower with a large number of blocks to achieve significant overhangs would require precision and stability. Nevertheless, the block-stacking problem serves as an entertaining and thought-provoking math puzzle that showcases the fascinating interplay between mathematics and physics.
When it comes to physics and mathematics, the concept of the center of mass and the harmonic series can open up a world of limitless possibilities. In idealized conditions where these principles reign supreme, the potential for exploration and discovery knows no bounds.
The Center of Mass
The center of mass is a crucial concept in physics that represents the average position of mass in an object. In simple terms, it is the point at which an object’s mass is evenly distributed in all directions. Understanding the center of mass is essential for analyzing the motion and stability of objects, as it plays a key role in determining how an object will move or behave in a given environment.
The Harmonic Series
The harmonic series is a fundamental mathematical concept that involves adding the reciprocals of natural numbers. This series has important applications in music, physics, and engineering, and its properties have been studied extensively by mathematicians throughout history. The harmonic series has intriguing properties, such as diverging to infinity, despite the fact that each term in the series approaches zero as n increases.
Endless Possibilities
When the center of mass and the harmonic series are combined in idealized conditions, the possibilities are truly endless. By leveraging these concepts, researchers and scientists can push the boundaries of what is possible in the fields of physics and mathematics. From designing more efficient structures to exploring the dynamics of complex systems, the center of mass and the harmonic series offer a wealth of opportunities for innovation and discovery.
In conclusion, the center of mass and the harmonic series are powerful tools that can unlock a world of possibilities in the realm of physics and mathematics. By understanding and harnessing these concepts, researchers can delve into new frontiers of knowledge and pave the way for groundbreaking advancements in science and technology.
The world of technology is constantly evolving, and with each passing day, new innovations are introduced that change the way we live, work, and communicate. One of the most exciting developments in recent years has been the rise of artificial intelligence (AI) and machine learning.
These technologies have the potential to revolutionize industries across the board, from healthcare and finance to transportation and entertainment. But what exactly is AI, and how does it work?
At its core, AI is a branch of computer science that focuses on creating systems that can perform tasks that typically require human intelligence. This can range from simple tasks such as recognizing speech or images to more complex tasks like driving a car or diagnosing diseases.
Machine learning, on the other hand, is a subset of AI that focuses on teaching computers to learn from data and make decisions without being explicitly programmed to do so. This is achieved through the use of algorithms that analyze large amounts of data to identify patterns and make predictions.
One of the key benefits of AI and machine learning is their ability to automate repetitive tasks and streamline processes, leading to increased efficiency and productivity. For example, in the healthcare industry, AI-powered systems can analyze medical images to detect diseases or assist doctors in diagnosing patients.
In the financial sector, AI algorithms can analyze market trends and make investment decisions faster and more accurately than human traders. And in transportation, self-driving cars are being developed that use AI to navigate roads and avoid accidents.
While the potential benefits of AI and machine learning are vast, there are also concerns about their impact on jobs and society as a whole. As these technologies become more advanced, there is a fear that they could replace human workers in certain industries, leading to job losses and economic instability.
There are also ethical concerns surrounding the use of AI, particularly when it comes to issues of privacy and bias. For example, AI algorithms have been known to perpetuate existing biases in data, leading to discriminatory outcomes in areas such as hiring and lending.
Despite these challenges, the potential of AI and machine learning to transform industries and improve our lives is undeniable. As we continue to push the boundaries of what is possible with these technologies, it is crucial that we also consider the ethical implications and ensure that they are used responsibly and for the greater good.