In a recent post, it was discussed how the deadweight loss resulting from a tax is directly proportional to the square of the tax rate. This means that if the tax rate is doubled, the deadweight loss quadruples. This relationship was demonstrated using basic algebra to prove the concept to students, as requested by an economist friend.
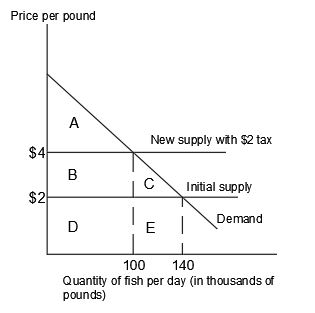
To begin with, let’s consider a scenario with a horizontal supply curve, as shown in the graph above, to calculate the Harberger triangle loss. In this case, the Harberger triangle loss is represented by the area denoted as C in the graph, which is equal to half of the base multiplied by the height. The height corresponds to the tax rate, denoted as t. To calculate the base, we need to determine the change in quantity demanded, referred to as delta Q.
Assuming the elasticity of demand is denoted as n, we can express it as the change in quantity demanded divided by the quantity demanded, divided by the change in price divided by the price. Therefore, delta Q/Q is equal to n multiplied by delta P/P. Subsequently, delta Q is equal to n multiplied by delta P/P multiplied by Q. Since delta P is equal to the tax rate t, we can express delta Q as n multiplied by t/P multiplied by Q.
Hence, the formula for the Harberger triangle loss can be derived as 1/2 multiplied by t squared multiplied by n/P multiplied by Q. This demonstrates the square relationship between the deadweight loss and the tax rate.
It is important to note that in cases where the supply curve is upward-sloping, the formula for calculating deadweight loss may be more complex. However, the fundamental square relationship between the deadweight loss and the tax rate still holds true.
Overall, understanding the relationship between tax rates and deadweight loss is crucial in analyzing the economic impacts of taxation policies. By recognizing the quadratic nature of this relationship, policymakers and economists can make more informed decisions regarding tax policy.