Solving Higher-Degree Polynomial Equations: A Breakthrough in Algebra
Norman Wildberger, a mathematician from the University of New South Wales (UNSW) in Australia, has achieved a remarkable feat by solving one of the oldest algebra problems – higher-degree polynomial equations. These complex calculations have baffled experts for nearly two centuries.
Teaming up with computer scientist Dean Rubine, Wildberger has detailed the groundbreaking method they used to crack these intricate equations in a recent paper.
Polynomials are equations that involve variables raised to non-negative powers (e.g., x3). When these powers are five or higher, they are classified as higher-degree polynomials.
While mathematicians have previously solved lower-degree polynomial equations, the higher-degree ones were deemed unsolvable according to the Abel–Ruffini theorem. Prior to this research, approximations were the only recourse.
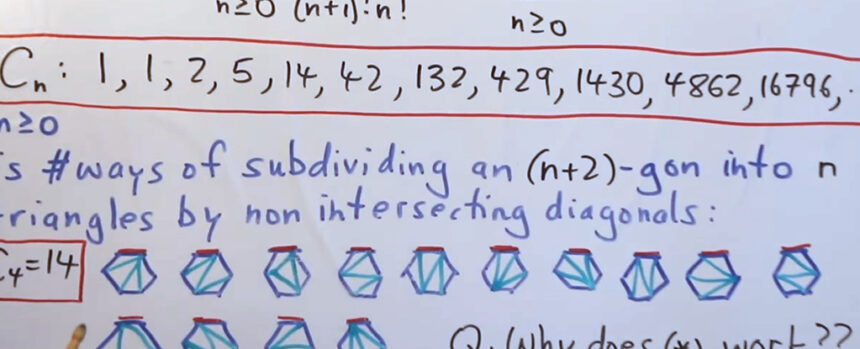
Wildberger and Rubine’s innovative approach leveraged Catalan numbers – a concept used in advanced number counting and arrangements, such as determining the number of ways polygons can be subdivided into triangles.
By expanding on the idea of Catalan numbers and extending polygon counts to various shapes beyond triangles, the researchers demonstrated that these numbers could serve as a foundation for solving polynomial equations of any degree. This method diverges from traditional approaches that rely on radical expressions like square roots and cube roots, instead embracing combinatorics – a more intricate form of counting.
The duo’s work was put to the test against classic polynomial equations, including a cubic equation famously studied by John Wallis. The results validated the efficacy of their new methodology.
Moreover, Wildberger and Rubine unearthed a novel mathematical structure known as the Geode, which intersects with Catalan numbers and appears to underpin them. This discovery holds immense potential for future research and discoveries.
Given the unprecedented nature of their approach, this breakthrough could prompt a reevaluation of fundamental concepts in mathematics, impacting computer algorithms, data structuring, game theory, and potentially even biology applications like counting RNA molecule folding.
Wildberger envisions widespread implications across various fields, stating, “This is a core computation for much of applied mathematics, so this is an opportunity for improving algorithms across a wide range of areas.”
The research findings have been published in The American Mathematical Monthly and mark a significant milestone in the realm of algebra.